一些簡單的凸分析
基本概念與基本性質
組合 Combination
Linear Combination 綫性組合:係數無要求;
Affine Combination 仿射組合:係數之和為1,可正可負;
Conical Combination 錐組合:係數為非负;
Convex Combination 凸組合:係數為非负,且和為1。
仿射函數/綫性函數
綫性函數:ax+by。綫性函數不可以有額外的常數項。
仿射函數:ax+by+c。仿射函數是綫性函數的平移。
在經濟學的語言中,常常將仿射函數稱爲綫性函數,從數學上來説這是不對的,但往往遵循慣例。
凸函數的幾何刻畫
凸函數常有兩種幾何刻畫:
-
兩點連綫處於函數圖像之上。
-
某點切綫位於函數圖像之下。
連綫、切綫只是一種廣義的説法,具體的形式因維度而定,例如在高維中的切綫其實是相切的超平面。
Chordal Slope Lemma
令(a,b)∈R為一個開區間,f:(a,b)→R為一個凸函數。則對於定義域內任何三個滿足x<y<z的點x,y,z∈(a,b)都有
y−xf(y)−f(x)≤z−xf(z)−f(x)≤z−yf(z)−f(y)
特別地,給定任何x0∈(a,b),函數x→x−x0f(x)−f(x0)是遞增的。
(三條綫各自均爲兩點連綫,可以將斜率處於中間的那條兩點連綫視爲斜率最陡峭和最平緩的兩條兩點連綫的加權平均,斜率處於中間者,是斜率最陡峭和最平緩的兩條兩點連綫拼接而成。)
證明:
y(z−x)===zy−xyzy−zx+zx−xyz(y−x)+x(z−y)
從而
y=z−xy−xz+z−xz−yx
其中z−xz−y=1−z−xy−x,
由x<y<z可知z−xy−x∈(0,1),從而上式即是將y表示成z和x的凸組合的表達式,根據f為凸函數,可知
f(y)≤=z−xy−xf(z)+z−xz−yf(x)z−xy−x(f(z)−f(x))+f(x)
從而
f(y)−f(x)≤z−xy−x(f(z)−f(x))
即
y−xf(y)−f(x)≤z−xf(z)−f(x)
但
f(y)≤z−xy−xf(z)+z−xz−yf(x)
又可以表示為
f(y)≤z−xz−y(f(x)−f(z))+f(z)
從而
x−zf(x)−f(z)≤z−yf(z)−f(y)
得證。
這意味著,當把x−h視為前麵的x、x視為前麵的y、x+h視為前麵的z時,有
f′(x−)=h→0limhf(x)−f(x−h)≤h→0limhf(x+h)−f(x)=f′(x+)
即凸函數任何內點x∈(a,b)的右極限總是不小於左極限,當屬於間斷點時右極限嚴格高於左極限。
進一步地
f′(x−)≤f′(x+)≤y−xf(y)−f(x)≤f′(y−)≤f′(y+)
因此,凸函數任何內點x∈(a,b)的左導數和右導數總是有界的:∣f′(x−)∣<∞,∣f′(x+)∣<∞從而上述命題凸函數內點的右極限總是不小於左極限,當屬於間斷點時右極限嚴格高於左極限中的“間斷點”可以進一步限製為跳躍間斷點(即凸函數的內點不會是無窮間斷點)。
Supergradient
参考 KC Border。
令 C 为 m 维欧氏空间的凸子集,f 为定义在 C 上的凹函数。称(同样为 m 维的)向量 p 是函数 f 在点 x∈C 处的 supergradient, 如果对于任何向量 y,都有 f(x)+p⋅(y−x)≥f(y)。
supergradient 是 gradient 概念的推广。
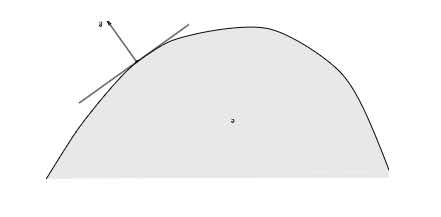
把不等式取相反符号,即为 subgradient。
命題:定義在開區間上的凸函數都是連續函數
令f:(a,b)→R為凸函數,則對於任何[x,xˉ]⊂(a,b),f都是李普希茨連續的,因此f在[x,xˉ]上也是絕對連續的。
證明:
(待補充)
命題
命題:凸函數的幾乎處處連續可微性質。
定義:極點 Extreme Point
令S⊂Rn為n維歐氏空間的凸子集,那些無法被S裏的點們由非平凡凸組合得到的點就是極點(這裏的平凡是指:就令所選取的點的權重為1,其他任意點的權重為0,依然是凸組合,但冇有實際意義)。如三角形的三個頂點、矩形的四個角、立方體的八個角等等都是極點。但任一條邊都可以被那條邊的端點組合而成,所以邊上的點不是極點。將S的極點們記為ext(S)。
凹凸性與擬凹凸性
凹凸性是基數性質,在單調變換下可能會發生改變。而擬凹凸性是敘述性質,可以在單調變化下保留。例如,無論是凹函數還是擬凹函數,在單調正變換后都將變成擬凹函數。
Polyhedra
給定超平面 H⊂Rd,記 H− 和 H+ 分別爲超平面的兩個閉半空間。至於是大於等於的記爲正、還是小於等於的記爲正具有任意性。一個 Polyhedron 是能被表示爲有限多個閉半空間的交集的集合。一個 Polytope 是有限多個點的凸包。一個 Polyhedral cone 是一個有限多個點的正包,即只要求係數爲正、不要求合爲一(因此不是凸包)。
凸集表示定理
凸集表示定理(一)Minkowski 定理
給定有限維嚮量空間E,X⊂E為緊凸子集,則對於任何x∈X,都存在有限個x1,...,xk∈ext(X)和正數μ1,...,μk滿足∑iμi=1,使得∑iμixi=x。
定義:表示 Representation
如前述Minkowski 定理中那般,對於某個x∈X,如果存在有限個x1,...,xk∈ext(X)和正數μ1,...,μk滿足∑iμi=1,使得∑iμixi=x,則稱x通過{μi}i得到了(凸)表示。
積分形式為:
對於定義在X上的任何連續線性(註意,這裏不限製為有限維空間,因此線性不意味著連續,而線性連續等價於線性有界)泛函f,和某個x∈X,如果f(x)=∫Xfdμ對於某個機率測度μ都成立,則稱x通過μ得到了表示。
因此Minkowski 定理也可以敘述為:
對於有限維嚮量空間中的緊凸子集,其任一元素都可以使用其極點得到表示。
凸集表示定理(二)Caratheodory 定理
對於任何有限維度n∈N,令S⊂Rn為n維歐氏空間的子集,則S的凸包co(S)中的任一點x∈co(S),都存在n+1個點{xi}i=1n+1⊂S和{λi}i=1n+1⊂[0,1](如果其中有某些λj=0,那就意味著隻需要少於n+1個xi),滿足∑i=1n+1λi=1(意味著權重非負、和為1,因此是凸組合),使得x=∑i=1n+1λixi。
即:對於任何有限n維空間裏的任一集合S,其凸包co(S)中的任一點都可由原S中不多於n+1個點的凸組合來表示。
證明:假設用了m≥n+2個點來做凸組合,即x=∑i=1mλixi,{xi}i=1m⊂S,{λi}i=1m⊂[0,1],∑i=1mλi=1。假設每個λi>0,∀i=1,...,m,否則有等於0的權重就意味著已經隻使用了少於m個點。
但即使{xi}i=1m不是線性相關的,任取一個xk,{xi−xk}i=k也是線性相關的,因此存在一組{μi}i=k,滿足μi∈[0,1]及∑i=kμi=1,並且μi不全為0,使得
i=k∑μi(xi−xk)=0
如果我們取μk=−∑i=kμi則有
∑i=1mμi=0
以及
0=i=k∑μi(xi−xk)===i=k∑μixi−i=k∑μixki=k∑μixi+μkxki=1∑mμixi
目前我們已經有了x=∑i=1mλixi和∑i=1mμixi=0,那麼對於任一實數α∈R都有
x=i=1∑mλixi−αi=1∑mμixi=i∑m(λi−αμi)xi
既然這個式子對任一α都成立,那麼我們可以選取特定的某個α,即
α=i=1,...,mmin{μiλi∣μi>0}
即隻在那些μi>0的組裏選,而xk,{xi−xk}i=k的線性相關保證了至少有一個μi>0。我們將這些μiλi中取到最小值的那一組記為第l組,那麼
α=μlλl
因此λi−αμi≥0,∀i,但λl−αμl=0。
這樣就把m個嚮量的凸組合變成了m−1個嚮量的凸組合。可以將這個過程一直持續下去。那麼這個過程應該到什麼時候停止呢?
應該到{xi−xk}i不再線性相關了為止。
而每個xi都是取自Rn,因此最多可以有n個線性不相關的xi=xi−xk,也就是最多可以有n+1個xj使得n個xi=xi−xk線性不相關,即要表示x,最多需要{xj}j=1n+1。當然,這隻是說最多需要n+1個,在不同的情景中可以隻需要更少,但永遠不需要更多。
特殊情況:邊界點
對於 S⊂Rn,記 C:=coS。如果 x∈C∩boudaryC,那麽如果想要將這種特別的 x 表示爲其它元素的凸組合,無需像 Carathedory 那樣要求 n+1 個元素,而只需 n 個就好了。
證明: 由於 x∈dbC,根據支撐超平面定理,存在超平面 Hs,r,其中 s=0,r∈R,使得
<s,x>−r=0
并且
<s,y>−r≤0,∀y∈C
由於 x∈C,根據 Caratheodory 定理,存在 x1∈S,...xi∈S,...,xn+1∈S 以及 α1>0,...αi>0,...,αn+1>0 使得 x=∑j=1n+1αjxj。代入 y=xj,得
0=<s,x>−r=j=1∑n+1αj(<s,xj>−r)≤0
因此必有 <s,xj>−r=0,∀j=1,...,n+1,這意味著每個 xj 都滿足超平面 Hs,r 的定義式 <s,x>−r=0。而超平面 Hs,r 的維度為 n−1 (x∈Rn 本身處於維度為 n 的空間内,<s,x>−r=0 的約束使得維度減 1)。
這表明 x 只需用超平面 Hs,r 上的點的凸組合,就可以表示。根據 Caratheodory 定理,x 可以表示為 (n−1)+1 個點的凸組合,得證。 □
凸集表示定理(三)Krein Milman 定理
-
版本一
對於任何非空緊凸集S⊂Rn,將S的極點們記為ext(S)={si}j,則co({si}i)=S。
-
版本二
證明:我們將採用歸納法證明。
當n=1時,非空緊凸集既是實端點的閉區間,其極點即是端點,極點的凸包即是這個區間。
假設對於n−1成立,我們表明對於n也成立。假設不成立,即S∖co(ext(S))=∅,那麼
結合Caratheodory定理和Krein Milman定理,可知在n維歐氏空間Rn中的任何非空緊凸集中的任一點,都可以被寫為其極點們中至多n+1個的凸組合。
凸集表示定理(四)Choquet integral representation
給定E為局部凸空間,X⊂E為可度量化的緊凸子集,任給x0∈X,都存在某個定義在X上的機率測度μ可以表示x0(意即f(x)=∫Xfdμ對於任何線性有界(从而连续)泛函f都成立)並且機率測度μ的支撐為X的極點(即{x∈X:μ(x)>0}=extX)。
Bauer 最大值原理
給定任何賦範線性空間X中的任何非空緊凸子集S⊂X,若f:S→R是上半連續(是semi,不是hemi)的凸函數(註意,這裏定義域是緊集,因此凸函數並不自動意味著連續函數),則集合S的極點ext(S)中至少存在一個點,使得函數f在該點取得最大值
argx∈Smaxf(x)∩ext(S)=∅
例子
(待補充)
(補上 Kleiner, A., Moldovanu, B., & Strack, P. (2020). Extreme Points and Majorization: Economic Applications. Available at SSRN.)
分離定理與支撐超平麵定理
(待補充)
分離超平麵定理
任取兩個非空凸集A,B⊂Rn,並且其中任一個具有非空內部,不妨令int(A)=∅,那麼A的內部int(A)與B不相交即int(A)∩B=∅當且僅當可以找到一個各分量不全為0的嚮量$v\in\mathbb{R}^{n}\setminus\lbrace 0\rbrace 和一個實數\alpha\in\mathbb{R}$使得
vTy≥α≥vTx,∀y∈B,x∈A
若從A的內部取點x∈int(A),則後一個不等號取嚴格
α>vTx,∀x∈int(A)
(若令int(B)=∅,則是前一個不等號取嚴格)
支撐超平麵定理
(待補充)
supporting hyperplanes to epigraphs
(待補充)
避免誤解
注意!!!儘管二階連續可微的函數 f:Rn→R 是凸函數當且僅當其海塞矩陣為半正定,但嚴格凸函數僅僅是海塞矩陣正定的必要而非充分條件,或者說海塞矩陣正定是嚴格凸函數的充分而非必要條件。
例如 f(x)=x4 是嚴格凸函數,但 f′′(0)=0。這是一個極其容易被誤用的性質!!!有很多老師會把嚴格凸函數時的海塞矩陣正定説成充要條件!!!這是錯的!!!
另外,“二階連續可微”這個性質也不可少。當然,可微性的假設要求定義域是開集,正如凸函數的假設要求定義域是凸集。
即使是一維歐式空間定義域(單變量)的嚴格凸函數,其充要條件也僅僅是 {x]inR:f′′(x)>0} 為稠密集而已!!!對於高維定義域(多變量)的嚴格凸函數,至今不存在任何通用的、簡化的充要條件刻畫!!!
(跑題一下,對於求解最優化問題來説,在 critical point 処的嚴格正/負定就足以作爲局部最優化的充分條件了,而無需在整個定義域都滿足嚴格正/負定,也無需凹凸性。但如果在整個定義域都滿足嚴格正/負定就可以談凹凸性和全局最優化了,儘管在整個定義域都滿足嚴格正/負定只是凹凸性的充分條件,也就意味著,有可能不滿足在整個定義域都嚴格正/負定但卻依然是嚴格凹凸函數,例如 f(x)=−x4 和 f(x)=x4 )
弱對偶定理
對於問題
x∈Rnsupf(x)s.t.gj(x)≥0,∀j∈{1,...,J}hl(x)=0,∀i∈{1,...,L}
其中,f(x)、{gj}j=1J和{hl}l=1L的凹凸性、可微性甚至連續性均不做要求。
這一問題可以採用對偶方式來求解,定義前述問題的值函數為p∗,則前述問題的對偶問題為
λ∈RJ,μ∈RLinfq(λ,μ)
其中
q(λ,μ)=x∈Rnsup(f(x)+λTg(x)+μTh(x))
由於q(λ,μ)(註意,q不是x的函數)是關於仿射函數λTg(x)+μTh(x)的逐點上確界,因此即使對f(x)、{gj}j=1J和{hl}l=1L的凹凸性不做任何要求,作為上確界函數(當能取到最值時,也就是關於參數λ和μ的最優值函數)這一點本身,使它成為了凸函數。
定義infλ∈RJ,μ∈RLq(λ,μ)問題的值函數為d∗,有如下定理
弱對偶定理
弱對偶定理:d∗≥p∗
證明:由於$g_{j}(x)\geq 0,\forall j\in\lbrace 1,…,J\rbrace 和h_{l}(x)= 0,\forall i\in\lbrace 1,…,L\rbrace ,所以對於任何x$,都有
f(x)≤f(x)+j∑λjgj(x)+l∑μlhl(x)
其中λj≥0,∀j以及μl≥0,∀l,從而
f(x)≤xsup{f(x)+j∑λjgj(x)+l∑μlhl(x)}=q(λ,μ),∀x
進而
supf(x)≤g(λ,μ),∀λ≥0,μ≥0
最終
p∗=supf(x)≤λ,μinfg(λ,μ)=d∗
超梯度與次梯度
(這個就是前面提到過的兩種幾何刻畫的第二種,即通過在該點処的切綫來刻畫。凸函數的切綫在函數圖像之上,凹函數的切綫在函數圖像之下。)
Thm1 凹函數在切線以下
假設函數f在x的一個凸開鄰域C⊂Rn上是凹的,並且在x點可微,則對於C中的任一y,都有
f(x)+f′(x)(y−x)≥f(y)
證明:任取y∈C,根據f在C上為凹函數,則對於任一λ∈[0,1]有
f(x+λ(y−x))=f((1−λ)x+λy)≥(1−λ)f(x)+λf(y)=f(x)+λ(f(y)−f(x))
特別地,選取λ>0並通除
λf(x+λ(y−x))−f(x)≥f(y)−f(x)
取λ>0趨嚮於0的單側極限,並根據f在x處可微,則有
f′(x)(y−x)≥f(y)−f(x)
即
f(x)+f′(x)(y−x)≥f(y)
意即,在x處,凹函數f(x)與仿射函數f(x)+f′(x)(y−x)(此時y=x,即f(x)=f(x)+f′(x)(x−x))相切,並在任何點y處,凹函數f(x)都在仿射函數f(x)+f′(x)(y−x)的下方。
Thm2
若f在凸開集U⊂Rn上可微,並假設對於任何x和y屬於C,都有f(x)+f′(x)(y−x)≥f(y),那麼f是凹函數。
證明:對於任何x∈C,定義仿射函數hx為hx=f(x)+f′(x)(y−x)≥f(y)。由於仿射函數(即不嚴謹的經濟學語言中的“線性函數”)是凹函數,並且根據假設,對於任何x∈C都有f≤hx,並且f(x)=hx(x),所以有
f=x∈Cinfhx
而一族凹函數的下確界仍然是凹函數,因此f是凹函數。
解讀:這意味著,我們可以用逐點取值不低於某一凹函數f的一族仿射函數hx來逼近(在下確界意義上)原函數f。f≤hx並且f(x)=hx(x)的這種關係,稱之為仿射函數hxmajorize函數f。註意,majorization是一個全局的性質,仿射函數hx在處處都不低於函數f,並在x處相切。
Def3
若一般地,不假設f的可微性,給定f是凸集C∈Rn上的凹函數,那麼我們稱一個嚮量p∈Rn是f在點x處的超梯度,若嚮量p滿足如下超梯度不等式:
f(x)+p(y−x)≥f(y)
對比Th1,可知超梯度p是f′(x)的推廣。並且對於給定的凹函數f和點x∈C,有可能存在多個嚮量pi都滿足超梯度不等式,即超梯度可以是個多點集∂f(x)={pi}i。函數在某點處超梯度的存在稱為該函數在該點超可微。
將f(x)+p(y−x)寫為f(x)+<p,y>−<p,x>,進而<p,y>−[<p,x>−f(x)]中括號中的部分在給定點x時為常數,這意味著,當給定x從而f(x)時,p是仿射函數f(x)+p(y−x)的斜率,這一斜率使得f(x)+p(y−x)是與f(y)在x處相切、並且處處不低於f的那些仿射函數中最低的一個。而截距項−[<p,x>−f(x)]便是使得f(y)≤<p,y>+α對於任何y都成立的最小的α。
Lemma4
Thm5 超可微性
凹函數在定義域的內點處都是超可微的。
證明:取定義域凸集C,並假設函數f在C上為凹函數,並且某點x屬於C的內點。則f的嚴格下圖S為
S={(y,α)∈C×R∣α<f(y)}
凹函數的下圖(及嚴格下圖)為凸集,即S為凸集。由於(x,f(x))不屬於S(被“嚴格”掉了),則根據分離超平麵定理,存在非0的法嚮量(p,λ)∈Rn×R將(x,f(x))與集合S分離開:
px+λf(x)≥py+λα
對於任何的(y,α)∈S,即y∈C且α<f(y)。
我們可以進一步限製法嚮量元素的符號:既然任何α<f(y)都需要滿足這一不等式,那麼令α為足夠大的負數,如果λ也是負數的話,不等式右端將會變得足夠大以至於不等式不能滿足,因此lamda≥0。(但無法取α為足夠大的正數,因為這樣將無法滿足α的選取條件,即α<f(y));
進一步地lambda也不能取0。如果λ=0的話,那麼不等式變為
px≥py
但由於x是C的內點,y=x±ϵz其中ϵ>0以及任一z∈Rn依然滿足y∈C,從而
px≥px±pϵz
進而pz=0,但由於z是任取的,隻能p=0。但這意味著“法嚮量”(p,λ)是零嚮量,矛盾。
因此λ>0。將不等式通除λ
f(x)+(−λp)(y−x)≥α
令α從下方(左側)趨近於f(x)
f(x)+(−λp)(y−x)≥f(y)
則超梯度不等式由超梯度−λp滿足,即凹函數f在點x處是超可微的。而點x是f的定義域內任一內點,因此凹函數f在其內點是超可微的。
註釋:在現代的凸分析中,凹/凸函數的定義域一般不是某個任一凸集C,而是一個特定的凸集Rn。並通過賦予Rn∖C中的點∞(凸函數)或−∞(凹函數)的方式,將定義域拓展到全空間Rn上去(並相應地將值域從實數域變為拓展後的實數域)。因此,若C的維度(定義為其仿射包aff(C)的維度)低於n,則定理中的“內點”在現代凸分析中,是指“相對內點”,即相對於其仿射包aff(C)而言的內點。
Def6 單側方嚮導數
定義函數f在點x處沿方嚮v的單側方嚮導數為
f′(x;v)=limλ>0,λ→0λf(x+λv)−f(x)
允許單側方嚮導數取值±∞
Lemma7
Lemma8 超梯度與單側方嚮導數
令f為凸集C上的凹函數,則
p∈∂f(x)當且僅當pv≥f′(x;v)對於任何使得x+v∈C的v∈R。
證明:
取x+v∈C,則對於λ∈[0,1]都有x+λv∈C。因此,如果p∈∂f(x),則根據超梯度不等式
f(x)+p(λv)p(λv)pvpv≥f(x+λv)≥f(x+λv)−f(x)≥λf(x+λv)−f(x)≥f′(x;v)
反之,如果p∈/∂f(x),則超梯度不等式對於p必然在至少一個滿足x+v∈C的v處不成立,即
f(x)+pv<f(x+v)
但由於f是凹函數,選定λ∈(0,1]有
f(x+λv)f(x+λv)f(x+λv)−f(x)λf(x+λv)−f(x)λf(x+λv)−f(x)=f((1−λ)x+λ(x+v))≥(1−λ)f(x)+λf(x+v)≥f(x)+λ[f(x+v)−f(x)]≥λ[f(x+v)−f(x)]≥f(x+v)−f(x)≥f(x+v)−f(x)>pv
意即f′(x;v)>pv。
Thm9 凹函數在某點處可微當且僅當該函數在該點處的超梯度為單點集。
即
Slater’s Condition
例子:效用最優化與成本最小化
應用:信息設計
一個發送者,一個接收者。有限的世界狀態空間Ω,發送者和接收者對世界狀態具有共同先驗μ0∈int(ΔΩ)。
發送者的vNM效用函數v:A×Ω→R,
接收者的vNM效用函數u:A×Ω→R。
發送者承諾(commit)一個信息結構(S,q),其中S為信號實現的可能集,為有限集;q:Ω→Δ(S)為條件機率。
接收者根據觀察到的信號實現s∈S和先驗信念p進行貝葉斯更新,並採取行動a∈A,其中A為接收者的有限行動空間。
接收者的行動同時影響發送者和接收者的效用。
接收者信念更新的形式為,對於任何ω∈Ω
μs(ω)=∑ω′∈Ωq(s∣ω′)μ0(ω′)q(s∣ω)μ0(ω)
根據這一後驗信念μs,接收者採取a^(s)∈A來求解如下問題
a∈Amaxs∈S∑u(a,ω)μs(ω)
預期到接收者的行為,發送者選擇並承諾信息結構(S,q)來求解如下問題
(S,q)maxω∈Ω∑s∈S∑v(a^(s),ω)q(s∣ω)μ0(ω)
但發送者的問題很不直觀,需要做如下簡化。我們在接收者問題中看到,當信息結構給定時,每個信號實現s對應於一個後驗信念μs,從而每個信息結構(S,q)根據不同的信號實現s∈S可以轉化為在一係列後驗信念{μs}s∈S上的分佈τ∈ΔΔ(Ω),τ(μs)=∑ω∈Ωq(s∣ω)μo(ω)。
在後驗信念的這個分佈上,貝葉斯可行總是成立的
s∈S∑μs(ω)ω′∈Ω∑q(s∣ω′)μ0(ω′)=s∈S∑∑ω′′∈Ωq(s∣ω′′)μ0(ω′′)q(s∣ω)μ0(ω)ω′∈Ω∑q(s∣ω′)μ0(ω′)=s∈S∑q(s∣ω)μ0(ω)=1⋅μ0(ω)
即後驗信念的期望等於先驗信念。
實際上,信號結構(S,q)與後驗信念上的分佈τ之間是雙射(bijection),即所有可能的信息結構可以被滿足貝葉斯可行的後驗信念上的分佈來表示
{τ∈ΔΔ(Ω)∣∫Δ(Ω)uτ(dμ)=μ0}
給定任何一個後驗信念μ∈supp(τ),接收者採取行動a^(μ),這樣就把接收者的行動規則從信號實現的函數變成了後驗信念的函數。
將a^(μ)代入發送者的效用函數,就可以把發送者的效用函數表示為接收者後驗信念的值函數
v^(μ)=ω∈Ω∑v(a^(μ),ω)μ(ω)
因此發送者的問題可以進一步表示為
τ∈ΔΔ(Ω)sup∫Δ(Ω)v^(μ)τ(dμ)s.t.∫Δ(Ω)μτ(dμ)=μ0
進一步定義函數v^(μ)的下圖的凸包
V=co({(v,μ)∈R×Δ(Ω)∣v≤v^(μ)})
對於接收者的任意後驗信念μ∈Δ(Ω),定義發送者效用值函數的凹化函數,
V(μ)=sup{v∈R∣(v,μ)∈V}
命題:發送者的問題可以進一步簡化為
V(μ)=τΔΔ(Ω)sup∫Δ(Ω)v^(μ)τ(dμ)s.t.∫Δ(Ω)μτ(dμ)=μ0
證明:我們先將發送者最終問題的值函數表示為W(μ),並表明W(μ)=V(μ)。
考慮發送者問題的對偶問題
D(λ)=τ∈ΔΔ(Ω)sup∫Δ(Ω)(v^(μ)−λTμ)τ(dμ)
根據弱對偶定理
D∗=λ∈R∣Ω∣infD(λ)≥W(μ0)
而v^的下圖的凸包V根據設定就是個內部非空int(V)=∅的凸集。
並且
V(μ0)=sup{v∈R∣(v,μ0)∈V}
同時,V(μ0)<v^(μ0)不成立,所以(μ0,V(μ0))∈V∖int(V)。
根據支撐超平麵定理,存在一個嚮量(比世界狀態空間的維度高一維)(u,w)∈R×R∣Ω∣滿足u>0使得
uV(μ0)+wTμ0≥uv^(μ)+wTμ
其中(v,μ)∈V。即使用支撐超平麵定理,表明(μ0,V(μ0))∈V∖int(V)與int(V)在(μ0,V(μ0))處存在支撐超平麵(u,w)。
(1) 如果V(μ0)=v^(μ0),那麼對於任何μ∈Δ(Ω),代入
uv^(μ0)+wTμ0≥uv^(μ)+wTμ
得到
v^(μ0)+u1wTμ0≥v^(μ)+u1wTμ
接下來我們表明τ=δ{μ0}(即不揭露任何信息,唯一地使接收者的後驗信念確定為先驗信念μ0)
在這種情況下(V(μ0)=v^(μ0))
對於發送者為唯一最優的
(即W(μ0)=v^(μ0)=V(μ0))。
根據
D(λ)=τ∈ΔΔ(Ω)sup∫Δ(Ω)(v^(μ)−λTμ)τ(dμ)
可知,如果能夠找到某個λ使得
δ{μ0}∈argτ∈ΔΔ(Ω)max∫Δ(Ω)(v^(μ)−λTμ)τ(dμ)
就可以了。但這就意味著找到了某個τ使得原問題的目標函數取得了D(λ)這個期望效用,那麼原問題目標函數的上確界值函數W(μ0)就至少為D(λ),即
W(μ0)≥D(λ)
但根據定義有
D∗=λ∈R∣Ω∣infD(λ)≥W(μ0)
因此
W(μ0)≥D(λ)≥D∗≥W(μ0)
即
W(μ0)=D(λ)
因此δ{μ0}確實解了原始問題。下麵我們考慮如何找到這個λ
令λ=−u1w
則
v^(μ0)+u1wTμ0≥v^(μ)+u1wTμ
變為
v^(μ0)+λTμ0≥v^(μ)+λTμ
兩邊同時積分,並代入τ=δ{μ0},有
∫Δ(Ω)(v^(μ0)−λTμ0)dμ0≥∫Δ(Ω)(v^(μ)−λTμ)τ′(dμ)
但這就意味著當λ=−u1w時,τ=δ{μ0}比任何其他的τ′∈ΔΔ(Ω)對於發送者來說都能帶來更高的效用。因此,當V(μ0)=v^(μ0)時,完全不披露任何信息,使得後驗信念與先驗信念完全重合是發送者的最優策略。
(2) 如果V(μ0)>v^(μ0),那麼根據Caratheodory定理,存在$\lbrace \hat{v}(\mu^{j}),\mu^{j}\rbrace _{j=1}^{|\Omega|+2}\subset\lbrace (v,\mu)\in\mathbb{R}\times\Delta(\Omega)|v\leq\hat{v}(\mu)\rbrace 和\alpha\in\Delta(\lbrace 1,…,|\Omega|+2\rbrace )$使得
j=1∑∣Ω∣+2αj(μj,v^(μj))=(μ0,V(μ0))
結合
uV(μ0)+wTμ0≥uv^(μ)+wTμ
可知
V(μ0)=v^(μj),∀j
以及
uV(μ0)+wTμ0=uv^(μj)+wTμj,∀j
從而
uv^(μj)+wTμj≥uv^(μ)+wTμ,∀j,∀μ∈ΔΔ(Ω)
取λ=−u1w,得
v^(μj)−λTμj≥v^(μ)−λTμ,∀j,∀μ∈ΔΔ(Ω)
由於{αj}j=1∣Ω∣+2是凸組合的係數,因此可以作為τ分配給μj的權重,即
τ(μj)=αj,∀j∈{1,...,∣Ω∣+2}
因此
∫Δ(Ω)(v^(μj)−λTμj)τ(dμj)≥∫Δ(Ω)(v^(μ)−λTμ)τ′(dμ),∀τ′∈ΔΔ(Ω)
從而{τ(μj)∣τ(μj)=αj,such that∑j=1∣Ω∣+2αj(μj,v^(μj))=(μ0,V(μ0))}j=1∣Ω∣+2確實解了原問題。因此W(μ0)=V(μ0)。
凸錐
凸錐是個凸集 S,需要滿足:其元素的任意縮放(無論是以 λ∈[0,1] 還是 λ≥1 的比率)仍然要在這個凸集内
λx∈S,∀λ≥0,∀x∈S
正極錐
给定一个錐 C={x},把那些對於錐中每個元素(向量) x∈C 都滿足 yTx≥0 的 y 們放在一起,就構成了它的正極錐 C+
C+={y:yTx≥0,∀x∈C}
yTx≥0 的條件意味著 y 跟 C 中每個元素的夾角都要小於或者等於 90 度。
負極錐(對偶錐)
C−={y:yTx≤0,∀x∈C}
yTx≤0 的條件意味著 y 跟 C 中每個元素的夾角都要大於或者等於 90 度。
舉例 1
錐 {b} 為一條射綫,那麽其對偶錐為 {b}⋆={y:yTb≤0} 即半空間。
舉例 2
对于任何 y∈Rn 来说,y1×nT0n×1≤0 恆(以等式)成立,因此退化的錐 {0} 的對偶錐 {0}⋆=Rn 為全空間。
相應地,向量 0n×1 是唯一能夠滿足對於任何 x∈Rn 都有 01×nTxn×1≤0 (以等式成立)的向量,從而 {Rn}⋆={0}
函數的凸化與凹化
函數的凸化或凹化即是函數上圖或下圖的凸集化。函數的凸化,是函數上圖的凸集化;函數的凹化,是函數下圖的凸集化。二者都是凸集化,并沒有“凹集”這種東西。
借助於單位形,Δk
Δk:={(α1,...,αk)∈Rk:j=1∑kαj=1,αj≥0,∀j=1,...,k}
Minorize by Affine Function
給定一個函數 g:Rn→R∪{+∞},并且要求其取值不可以恆爲 +∞。如果對於某對 (s,b)∈Rn×R,有
g(x)≥<s,x>−b,∀x∈Rn
則稱仿射函數 <s,x>−b minorize 了函數 g。
凸化定理
對於可以被某個 (s,b) 所代表的仿射函數所 minorize 的、滿足前述要求的函數 g 來説,可以定義如下三個函數 f1,f2,f3,并且這三個函數在 R 上是等價的
-
f1(x):=inf{r:(x,r)∈co epig}
-
f2(x):=sup{h(x):h∈Convex functions in Rn,h≤g}
-
f3(x):=inf{∑j=1kαjg(xj):k=1,2,...;xj∈domg,∑j=1kαjxj=x}
這個 ∑j=1kαjxj=x 條件無論是在 minorization 還是 majorization 裏都是需要滿足的。這個條件在經濟學裏的運用,比如,後驗信念 xj 們的期望等於先驗信念 x。
反過來看,也可以視爲將先驗信念 x 分解為 k 個後驗信念 xj,j=1,...,k,其係數分別為 αj,j=1,...,k。
證明
將那些 minorize 了 g 的凸函數們(任何凸函數,不必是仿射函數)組成一個集合,記爲 Γ。
由於仿射函數本身也是凸函數,所以至少仿射函數可以 minorize 函數 g,所以 Γ 不是空集。
-
f1(x) 是一個凸集 co epig 的下確界函數,因此 f1(x) 是一個凸函數。
-
接下來我們證明 f2≤f1,∀x
對於任一 h∈Γ,考慮它的上圖 epih。既然 epih 本身就是 h 的上圖,那麽由其定義的下確界函數 lepih 就是 h 本身。既然 h≤g,那麽 g 的上圖 epig 是包含在 h 的上圖之内的,并且由於 epih 是個包含 epig 在内的凸集,因此 epih 也包含 co epig 在内,所以
h=lepih≤lco epig=f1
由於這個不等式是對任一 h∈ConvRn 都成立的,那麽必然也對 f2(x):=sup{h(x):h∈Convex functions in Rn,h≤g} 成立。
- 接下來我們證明 f3≤f2,∀x
我們采用的方式是表明 f3∈Γ。我們表明 f3≤g:當 k=1 時,inf{∑j=1kαjg(xj):k=1,2,...;xj∈domg,∑j=1kxj=x}≤αα=1g(x)≤g(x),因此,如果 f3∈ConvRn,那么 f3 就是一个 minorize 了 g 的凸函數,所以 f3∈Γ,那麽 f3 肯定也不會大於 Γ 裏面的上確界,即 f2,則有 f3≤f2。那麽如何表明 f3 是個凸函數呢?
首先,由於存在某個 (s,b) 來 minorize g,這意味著要對於每個 x 都成立,即對於每個 x 都有 g(x)≥<s,x>−b。那麽既然對於每個 x 都成立,也就當然有
j=1∑kαjg(xj)≥j=1∑kαj(<s,xj>−b)=<s,x>−b
即 f3 是被仿射函數 <s,⋅>−b 所 minorize 了的。
現在從 f3 的嚴格上圖裏選取兩個點 (x,r) 和 (x′,r′),即使得 f3(x)<r 和 f3(x′)<r′ 的 (x,r) 和 $(x^{\prime}。根據 f3 的定義,這意味著存在某個 (k,{αj},{xj}) 和 (k′,{αj′},{xj′}) 使得
j=1∑kαjg(xj)<r
和
j=1∑kαj′g(xj′)<r′
對於任何 t∈(0,1) 來説,做二者的嚴格凸組合,有
tj=1∑kαjg(xj)+(1−t)j=1∑kαj′g(xj′)<tr+(1−t)t′
注意
tj=1∑kαjxj+(1−t)j=1∑kαj′xj′=tx+(1−t)x′
可以把左側視爲對 tx+(1−t)x′ 凸分解為 k+k′ 個元素。根據 f3 的定義,有
f3(tx+(1−t)x′)≤tj=1∑kαjxj+(1−t)j=1∑kαj′xj′=tx+(1−t)x′
這就意味著 f3 的上圖是凸集,從而 f3 是個凸函數。
- 接下來我們證明 f1≤f3。任選定義域内的一個點 x∈Rn,以及 x 的一個凸分解 x=∑j=1kαjxj。
根據定義,(xj,g(xj))∈epig,∀j=1,...,k,那麽根據構造凸包的方法
(x,j=1∑kαjg(xj))∈co epig
即
f1(x):=inf{r:(x,r)∈co epig}≤j=1∑kαjg(xj)
由于這個凸分解是任意的,那麽對於凸分解中的下碻界 f3 也應該是成立的。□
epi(cog)=co(epig)
需要截断下部分。
∑j=1kαjxj=x 使得 x 為邊界點,根據 Caratheodory 定理在邊界點的特殊情況,k≤n+1。
參考文獻
[1] Vohra, R. V. (2004). Advanced mathematical economics. Routledge.
[2] Kamenica, E., & Gentzkow, M. (2011). Bayesian persuasion. American Economic Review, 101(6), 2590-2615.
[3] Kai Hao Yang’s Lecture Notes

